这也算是一篇鸽了很久的文章,应该很早就打算写的,这篇论文非常有意思,原文在这里Improving Approximate Nearest Neighbor Search through Learned Adaptive Early Termination。其中的作者之一是Mingjia Zhang,现在在微软亚洲研究院,发表了不少有关ANN的文章。如果对ANN还不太清楚的小伙伴可以先看下我之前写的这篇文章。
背景
由于我们考虑的是Approximate Nearest Neighbor,这一类查询特点是没有一个所谓的理论误差界限,只能通过人工调参去保证精度和性能之间的trade-off。衡量ANN索引性能的时候,我们会使用一些测试向量,通过调整搜索参数,来控制查询过程中搜索的范围(即访问的数据库子集的大小),最后我们会画出一条精度和性能相关的曲线,精度越高,性能就越差。基于真实业务所需要的精度,我们就可以得到“合理”的参数设置。
但是这种固定参数的设置显然是有overhead,因为我们“公平”地对待了所有的查询向量,但显然对于某些“简单”的查询而言,一个较小的参数就已经找到了正确的近邻,而调大参数获得收益的只是很少一部分“困难”的查询。比如我们现在使用较小的参数,访问了10%的数据,得到了98%的精度,而统一调整成较大的参数,访问了50%的数据,得到了99%的精度,这说明只有1%的查询精度受益,但是查询性能却严重下降,这也是ANN索引一个典型的长尾效应。
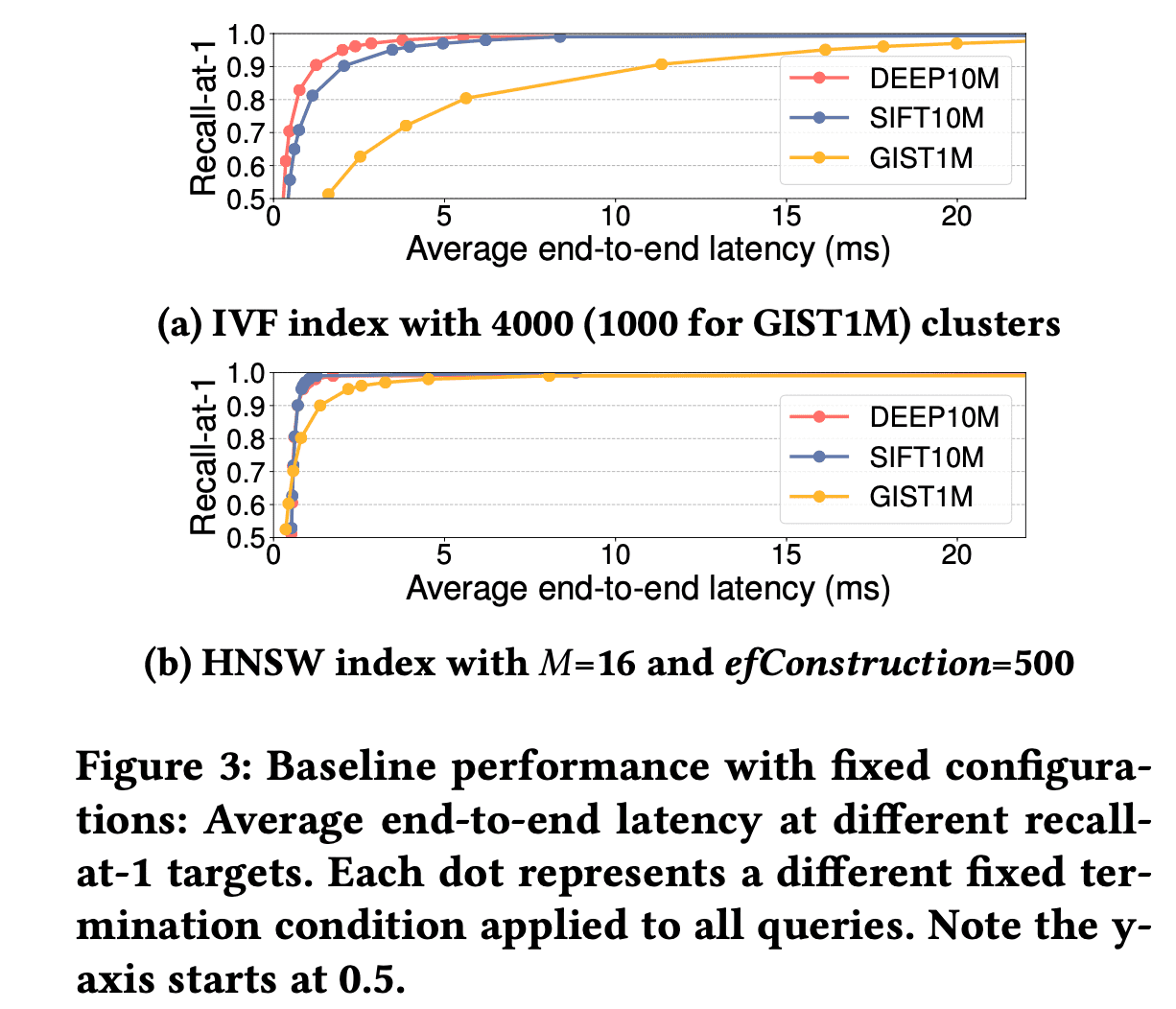
作者通过详实的实验论证了这个观点,使得论文的motivation部分可读性很高。作者基于HNSW图索引(调整ef参数)和IVF索引(调整nprobe参数)两种典型的索引展开实验,首先在最近邻(即1NN)场景下说明了固定参数设置下,后期精度的提升会带来性能的严重下降,比如在GIST1M数据集上使用HNSW索引,只要0.807ms就可以达到0.8的精度,但需要2.185ms才能达到0.95。另外给出了每个测试向量找到最近邻需要在索引上访问的数据点,大部分测试向量都比较集中在较小的范围,比如在DEEP1M数据集上构建HNSW索引,80%的测试向量只需要在图上访问少于547个数据点,只有剩余20%测试向量需要在索引上访问很多数据才找到ground truth,这个数字可以高达88696个数据点。
 | 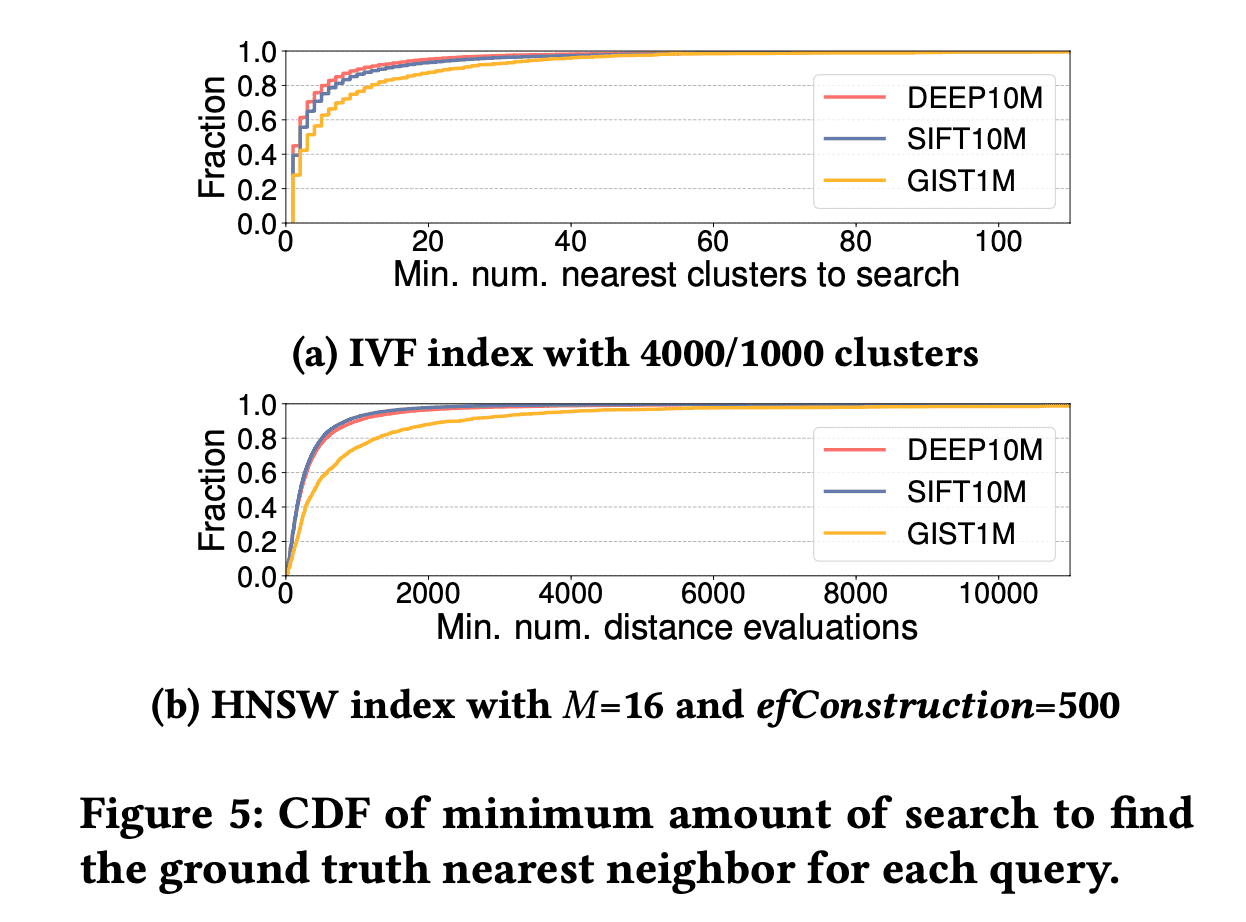 |
这说明为每个测试向量设置一个Learned的参数很有必要,但是作者更进一步,汲取了数据库优化器里Adaptive Query Processing的思想, 可以把查询的中间结果纳入考虑,把运行中的metrics作为指导后续参数设置的重要依据。作者验证了一下,如上文所说80%向量只需要访问少于547个数据点,所有测试向量均以访问547个数据点作为基础,然后来看测试向量和当前执行过程中的“最近邻”的距离dist,和接下来还需要访问的数据点个数n之间的关系,可以发现一个明显的规律就是,dist越小,n也就越小,所以作者认为可以首先对所有测试向量设置一个统一的可以接受的较小的参数,在运行完之后,通过中间结果指标再来为每个查询设置合适的参数继续执行或者中止。
方法
Motivation部分基本就已经把作者接下来的思路说的差不多了。从大体框架上而言,我们会训练一个模型,最终的输出是一个索引的搜索参数,对于不同的索引,这个参数可能具体含义是不同的,但是归根到底这个结果反映的是查询过程访问数据量的大小。
输入信息分为三个:测试向量,索引结构,查询的中间结果特征。
IVF索引
IVF类的索引基本思想就是把向量通过聚类算法分成若干个聚类,实际查询时通过调整nprobe参数(需要访问的最近的几个聚类)控制搜索范围。
除了测试向量外,加入5个其他特征:测试向量最近的聚类距离c_1st和第10,20...近的聚类c_xth的比值,基于统一的nprobe参数进行查询以后,测试向量和当前的第一和第十的近邻的距离d_1st和d_10th,,上述两个特征的比值d_1st/d_10th,以及测试向量和当前最近邻的距离和最近聚类距离的比值d_1st/c_1st。作者通过是否加特征的模型精度验证了中间结果特征是有效的。
 |  |
那么统一的基础参数应该如何设置?太小会影响模型精度,太大会使性能下降。作者采用grid search的方式,相当于尝试了不同参数下的端到端结果,选取一个较为合适的。
HNSW索引
HNSW是一种非常流行的图索引。由于图索引上的ef参数是搜索时保存中间结果的优先级队列的大小,但它其实和查询过程中搜索数据量的大小并没有理论上的线性关系保证,而查询耗时主要是在搜索中向量的距离计算,所以直接选取距离计算次数,即查询过程中访问数据量的大小作为模型训练目标更加合适一些。
类似地,加入了5个其他特征:搜索到HNSW图的最底层的时候的向量和测试向量的距离d_start,基于统一的参数进行查询以后,测试向量和当前的第一和第十的近邻距离d_1st和d_10th,以及d_1st和d_10th分别对比d_start的比值。
 |  |
训练中也有一些小问题,比如图索引连通性的本质缺陷,可能有些测试向量访问了所有reachable的数据都没能找到正确的最近邻,在训练时把它们从训练集中移除。 另外由于访问数据量这个值可能会有很大的范围,作者用log2(num)作为模型输出的结果,使得模型更容易收敛。
实验
实验部分就不过多展开了,其实作者在展示方法的时候已经说明了模型是有用的。在实验部分更多的是展示端到端的查询性能。主要比较了在无数据压缩场景下DEEP10M,SIFT10M,GIST1M数据集上,HNSW和IVF采用adaptive方式的效果。同时还比较了在OPQ压缩算法场景下,DEEP1B和SIFT1B数据集上采用该方法的效果。感兴趣的读者可以看论文实验部分获取更多细节。
总结
这篇论文的idea是很“simple”的,但是带来的收益是很明显的,尤其是对精度要求较高的ANN查询场景。而且论文的写作水平很高,可读性很强。大家(比如我。。)可能也会发现参数的设置对每个测试向量的影响是不同的,企图去找到一点原因,但可能没想到说用学习型的方法去为每一个查询做参数设置。
但是最后还是有很多讨论的空间,比如文章里只是对最近邻这个问题进行了讨论,包括模型的训练都是基于这个条件来做的,那么是否能够比较好地应用到KNN的场景,这对真实场景下的使用很重要。Naive的方式当然是针对不同的K,进行模型的训练和推导,但这个开销显然是不可接受的。也许针对最近邻训练的模型可以有一定的通用性(保持各个测试向量的参数设置比例不变,进行同比例的放缩),可能对5NN有用,但对50NN也许就不再适用了。这个问题相当于是输入更复杂了,不仅针对某个测试向量,还有对于我们要的近邻个数K,来给出一个adaptive的参数设置。
还有一点是说这里的模型和索引是强相关的,相同的数据下比如构建了一个HNSW索引,在此基础上训练出来的模型只适用于这个HNSW索引。如果我另外再建一个HNSW索引就不行了,在前面索引上可能“困难”的查询现在就变得“简单”了,这样也引出一个很有趣的问题:这样的信息输入是否可以指导“tune”索引让索引本身变得更强大。或者训练一系列索引,让测试向量去选择一个最合适的。